A több ismeretlent tartalmazó összetett egyenletek, a trigonometrikus számítások, az elméleti fizika, a lineáris algebra, a valós számok, a differenciálegyenletek és a matematikai tételek az őskortól kezdve egészen a 20. század legújabb felfedezéseiig alapjaiban formálták át világunkat.
Minden egyes új matematikai egyenlet a fizikai világunkkal kapcsolatos új kérdésekkel és válaszokkal áraszt el minket.
Ebből kifolyólag ebben a cikkben egy válogatást találsz az olyan matematikai egyenletekből, amelyek rányomták bélyegüket a korszakukra, és alapvetően változtatták meg a matematikáról, a tudományról, sőt néha még a világról való gondolkodásunkat is.
Ha továbbra is bonyolultnak tűnik, ne habozz fel keresni egy matektanárt.


1. Pitagorasz-tétel: egy alapvető matematikai állítás
Ez az i.e. 6. század óta használt tétel valószínűleg az egyik legismertebb a világon, és továbbra is a modern matematika egyik alappillére, amely hosszú időn keresztül hozzájárult a tudományág fejlődéséhez és a matematika történetéhez.
A Pitagorasz-tétel fogalma a matekórák nélküli évek után is ott lapul a memóriánk egy kis szegletében. Még ha egyeseknek rossz emlékeket is idéz fel, a tételt alkotó elemek, illetve azok jelöléseit nehéz elfelejteni.
Próbáljuk meg együtt felidézni a Pitagorasz-tétel pontos definícióját:
Bármely derékszögű háromszög átfogójának (a leghosszabb, a derékszöggel szemben lévő oldal) négyzete egyenlő a másik két oldal (befogók) négyzetösszegével.
A fordított Pitagorasz-tétel ebből kiindulva azt próbálja bizonyítani, hogy egy háromszög derékszögű, ha
egy háromszög egyik oldalának négyzete egyenlő a másik két oldal négyzeteinek összegével.
A tétel, annak megfordítása és a hozzá kapcsolódó híres egyenlet (a2 + b2 = c2) új szemszögből vizsgálta az általános síkgeometriát.
A híres Pitagorasz-tétel egyenletének köszönhetően ma már könnyű kiszámítani a hosszúságokat és szögeket, valamint bebizonyítani, hogy egy háromszög derékszögű-e vagy sem.
A Pitagorasz-tételt ma is használják olyan gyakorlati területeken, mint az építőipar és az építészet, az asztalos szakmák vagy a kertészet. Mindez csak néhány példa, szóval a lista korántsem teljes!
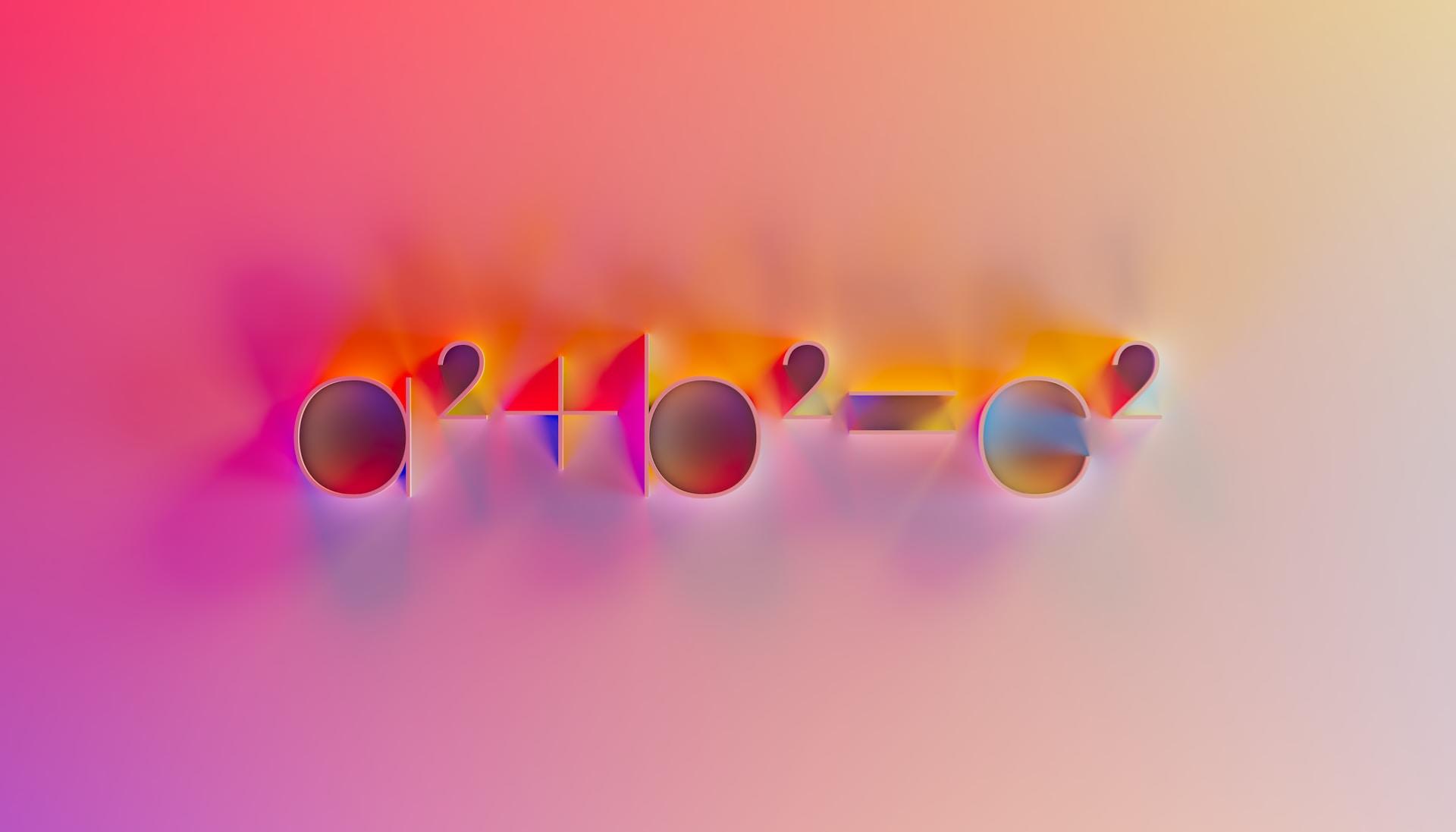
2. Thalész-tétel: egy másik alapvető matematikai állítás
Thalész híres tétele a Pitagorasz-tételhez hasonlóan szintén a felső tagozatos matekórák egyik pillére.
A piramisok magasságának megméréséről szóló legendák is Thalész nevéhez fűződnek – erre még később visszatérünk. Előtte azonban szánjunk néhány másodpercet erre a tételre, amely sokaknak okozott már rémálmokat.
A Thalész-tétel definíciója:
Ha egy kör átmérőjének két végpontját összekötjük a kör kerületének bármely más pontjával, akkor derékszögű háromszöget kapunk.
A tétel megfordításával azt bizonyíthatjuk be, hogy a derékszögű háromszög köré írt kör középpontja az átfogó felezőpontjában van.
De hogyan forradalmasította a Thalész-tétel a matematikát, és milyen módon nyújtott valódi matematikai megoldást konkrét problémákra?
A geometriában Thalész tétele és annak megfordítása használható az egyenesbe elrendezés vagy párhuzamosság feltételeinek bemutatására és megállapítására.
Az egyiptomi piramisokhoz visszatérve a legenda szerint Thalész II. Jahmesz (Ahmosze) egyiptomi fáraó kérésére Egyiptomba utazott, hogy kiszámolja a piramisok, pontosabban a Kheopsz (gízai nagy) piramis magasságát. Délben, amikor botjának árnyéka egyenlő volt a bot magasságával, függőlegesen a földbe szúrta azt, és így szólt a fáraóhoz:
Az árnyékommal való kapcsolatom ugyanaz, mint a piramisnak a sajátjával való kapcsolata.
Más szóval, ha ismerjük a bot hosszát és az árnyékát, akkor ugyanezeket az arányokat használhatjuk a piramisok magasságának meghatározásához, miután megmértük az árnyékukat.
3. Logaritmusok
A John Napier skót matematikus és teológus által 1610-ben népszerűsített logaritmusok az inverz függvényeket, a számok ellentetjét és az exponenciális függvényeket foglalják össze.

A számítógép kifejlesztéséig a logaritmusokkal való számolás volt a legáltalánosabb módja a nagy számok összeszorzásának, ami a gyorsabb számolás mellett azt is lehetővé tette, hogy óriási előrelépéseket érjünk el a matematika, a fizika, vagy akár a mérnöki tudományok és a csillagászat területén is.
A logaritmus definíciója:
A logaritmus az az exponens vagy hatvány, amelyre egy bázist (alapot) emelni kell ahhoz, hogy egy adott számot kapjunk.
A logaritmusoknak 3 típusa van:
- természetes logaritmus: a matematikai analízis alapja
- decimális logaritmus: matematikai számításokban
- bináris logaritmus: számos alkalmazási területen hasznos, például az elméleti számítástechnikában
Logaritmus példa 10-es bázisú logaritmus (log) esetében:
log (1) = 0, log (10) = 1, log (100) = 2.

4. Relativitáselmélet
Függetlenül attól, hogy valaki járatos-e a matematikában és a fizikában vagy éppen halvány fogalma sincs a matekban használatos terminológiáról, mindenki ismeri Albert Einstein híres E = mc² képletét, amely a feje tetejére állította a fizika minden eddig ismert szabályát.
Einstein képlete ma is kulcsfontosságú, mert megmutatja, hogy az anyag és az energia kölcsönösen átalakíthatók. Speciális relativitáselméletével bevezette azt az elképzelést, hogy a fénysebesség egy egyetemes állandó, amely nem változik, és hogy az idő múlása nem azonos a különböző sebességgel haladó emberek esetében. A szintén általa kidolgozott általános relativitáselmélet egyszerűen olyan gravitációról szól, amelyben a tér és az idő görbül és meghajlik. Ez jelentős változás volt Newton gravitációs törvényéhez képest.
Einstein relativitáselmélete még ma is alapvető fontosságú a világegyetem eredetének, szerkezetének és sorsának megértéséhez.

Mindez jól tükrözi, hogy a matek lehetővé teszi számunkra a világ megértését. Íme hát egy újabb bizonyíték – ha egyáltalán még mindig szükséges – a matematika jelenlétéről a mindennapi életben.
Kiváló matektanárok szintén megtalálhatóak platformunkon.
5. A Newton-féle gravitációs törvény
Ki ne hallott volna már Isaac Newton gravitációs törvényéről?
Ismered a történetet az almáról, ami a tudós fejére esett, miközben a Holdat csodálta az égen? A történet 1687-re nyúlik vissza: a két test (a Hold és az alma) összehasonlítása elgondolkodtatta Newtont, hogy vajon az almával ellentétben miért nem esik le a Hold.
A válasz nyilvánvaló: egy gravitációs erőnek köszönhetően. Így jött létre a híres Newton-féle gravitációs törvény, miszerint:
Bármely két test kölcsönösen vonzza egymást. A csillagok a tömegük szorzatával arányosan vonzzák egymást, ami fordítottan arányos a köztük lévő távolság négyzetével.
Más szóval két pontszerűnek tekinthető test között ez az erő egyenesen arányos a tömegek szorzatával, és fordítottan arányos a köztük lévő távolság négyzetével. Képlete:

Az F itt a gravitációs erőt, G a gravitációs állandót, m1 és m2 a testek tömege kilogrammban, az r pedig a tömegek középpontja közötti távolságot jelenti méterben. A fenti képlet tehát az egyik test másik testre (és fordítva) kifejtett erő értékét próbálja bizonyítani.
A Newton-féle gravitációs törvény elméletét 200 évvel később Einstein relativitáselmélete váltotta fel.
Vajon a szerelem és a matek között van kapcsolat? Ebből a cikkünkből kiderül.

6. Infinitezimális számítás
Az algebra és a geometria között félúton az infinitezimális számítás (differenciál- és integrálszámítás) a matematika önálló ága, amely a függvények tulajdonságait és viselkedését, illetve azok deriváltját és határértékeit vizsgálja.
Ha az infinitezimális számítást egyetlen pontban kellene összefoglalni, akkor az a változók tanulmányozása lenne.
A gyakorlatban számos konkrét alkalmazása van kezdve a mechanikától a fizikán át egészen a közgazdaságtanig. A különféle adatok széleskörű figyelembevételével a változók tanulmányozása lehetővé teszi például egy vállalat fejlődésének elemzését és annak pénzügyi erejének felvázolását az elkövetkező évekre vonatkozóan.
7. Az Euler-összefüggés
Az Euler-összefüggést a matek egyik gyöngyszemének tartják, mert olyan matematikai állandók valószínűtlen kombinációja szerepel benne, mint a pí, az Euler-szám (e) és a képzeletbeli egység (i), valamint az aritmetika három alapvető matematikai művelete, nevezetesen az összeadás, a szorzás és a hatványozás.
Az összefüggés névadója a svájci matematikus Leonhard Euler, aki észrevételeit a Bevezetés a végtelenek analízisébe (Introductio in analysin infinitorum) című művében, a matematikai analízis valóságos bibliájában emelte ki.
Miért kápráztat el oly sokakat ez az egyenlet? Mert az aritmetika alapvető műveletei közül hármat is használ, nevezetesen az összeadást, a szorzást és a hatványozást, és önmagában összefoglalja a matematika nagy részét:
- Az e a természetes logaritmus alapját képező matematikai állandó (értéke kb. 2,71828), amelyet az analízisben és a differenciálszámításban használnak.
- Az i képzeletbeli egység, az algebrát jelképezi (a 3 ismeretlent tartalmazó egyenletekben található komplex számok forrása).
- A titokzatos pí a geometriát reprezentálja.
- A 0 mint az összeadás semleges eleme és az 1 mint a szorzás semleges eleme az aritmetikát és a matematikát képviselik.
Az Euler-összefüggés megnyitotta az utat a topológia, a modern matematika egyik ágának fejlődése előtt.
Összefoglaló:
- Amint azt az idők során, különösen a 18. és 19. század óta láthattuk, a matematikai egyenletek képesek voltak átalakítani a világot, amelyben élünk, bizonyos esetekben megváltoztatták gondolkodásmódunkat, és más irányba terelték a világ alakulását.
- Egy biztos, akár tetszik, akár nem, ezek az egyenletek a matematikával együtt mindenütt jelen vannak, és rendszeresen alkalmazzuk őket a mindennapi élet számos területén.
Vajon mi lesz a következő matematikai innováció? Milyen új matematikai felfedezés fogja ismét a feje tetejére állítani az életről alkotott elképzeléseinket?
Nyugodt lehetsz, mert a Superprof csapata résen lesz, és tájékoztatni fog miden újdonságról.
Ha szívesen olvasnál még a matekról, vess egy pillantást azokra a cikkeinkre is, amelyeben azt taglaljuk, hogyan használható a matek a pókerben.
Összefoglalás AI segítségével














