Javuló teljesítmény, új kütyük, technikai forradalom: ezek az újdonságok az amatőr sportot is érintik. A matematikusok is sokféleképpen foglalkoznak a sporttal és a teljesítménnyel. Azt gondolnád, hogy a mateknak és a sportnak közük sincs egymáshoz? Nagyobbat nem is tévedhetnél!
Hogy fokozd a sport, a matematika vagy mindkettő iránti szenvedélyedet, olvasd el ezt a cikket a matematika szerepéről a sportban!

Geometriai számítások kosárlabdában, golfban és síelésben
A matematika elengedhetetlen a golfban a távolság, a szög és a lendítés röppályájának kiszámításához.
A játékosok geometriai számításokat használnak a távolságok felmérésére, és az ütéseket a terep magasságának megfelelően igazítják. A matematikai pontosság segít a játékstratégia javításában, figyelembe véve az időjárási viszonyokat és a pályán található akadályokat.

A matematikai ismeretek a kosárlabdában is jól jönnek, például az optimális dobási szög és ív meghatározásában, míg síelésben a lejtők dőlésszögének és ívének megértését szolgálja a sebesség fokozása és a pályán való irányítás fenntartása érdekében.
Parabolikus röppálya kiszámítása kosárlabdában
A kosárlabda röppályája egy parabolikus görbét követ, amelyet egy kvadratikus egyenlet ábrázol:

Ahhoz, hogy megértsük ezt a pályát, három kulcsfontosságú paramétert kell mérnünk:
- az indítási szöget (θ),
- a kezdeti sebességet (v0),
- a labda kezdeti magasságát (h).
Tegyük fel, hogy a labdát 45°-os szögben, 8 m/s kezdősebességgel, 2 méter magasból dobod. A függőleges helyzetet a vízszintes távolság függvényében a következő egyenlet adja meg:
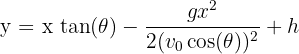
ahol a gravitációs gyorsulás (g) megközelítőleg 8/s.
Kezdésként dobd el a labdát, és mérd meg a dobásod paramétereit.
Ha például 45°-os szöget és 8 m/s kezdeti sebességet mérsz, ezeket az értékeket beillesztheted az egyenletbe, hogy megjósold a röppályát. A képlet a következő lesz:
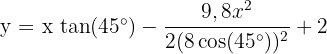
Ezután menj ki a pályára, és végezz néhány dobást. Jegyezd fel, hol landol a labda és milyen magasra jutott. Ha például egy 45°-os szögben, 4 méteres sebességgel indított labda számított maximális magassága 4 méter, akkor ezt az értéket össze lehet hasonlítani a megfigyelésekkel.

Az elméleti görbét grafikonpapíron vagy egy grafikus alkalmazás segítségével ábrázolva megjelenítheted a számítások által előre jelzett pályát, és összehasonlíthatod azt a tényleges pályával. Ez lehetővé teszi a mérések és paraméterek beállítását a dobások pontosságának javítása érdekében. Láthatod hát, hogy a matek tényleg mindenütt jelen van és nem lehet elég korán kezdeni!
🏀 Még jobb, hogy az olyan játékosok potenciálját is meghatározhatod vele, mint Michael Jordan!
A Pitagorasz-tétel a golfban
A Pitagorasz-tétel egy matematikai szabály két pont távolságának kiszámítására kétdimenziós térben, ami nagyon hasznos a golfpályán való távolságbecsléshez.
A Pitagorasz-tétel reciproka azt mondja ki, hogy ha az átfogó négyzete egyenlő a két befogó négyzeteinek összegével, akkor a háromszög derékszögű. Más szóval, ez egy módja annak ellenőrzésére, hogy derékszögű háromszöggel van-e dolgunk.
Superprofos matekóra
A Pitagorasz-tétel szerint egy derékszögű háromszögben az átfogó (a derékszöggel szemben lévő oldal) négyzete egyenlő a másik két oldal négyzeteinek összegével. Ha tehát az átfogó a c és és a másik két oldal az a és b, akkor ezt a következőképp fejezhetjük ki:
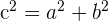
Képzeld el, hogy a golfpályán vagy, és ki akarod számolni a labda és a lyuk közötti távolságot. Tudod, hogy:
- a = A vízszintes távolság (egyik útvonaljelzőtől a másikig) 150 méter.
- b = A függőleges távolság (enyhén emelkedett helyzetből) 40 méter.
- A közvetlen távolság meghatározásához a Pitagorasz-tételt kell alkalmazni.

Az egyenletet használva ez így néz ki:
- c2 = 1 502 + 402
- c2 = 22 500 +1 600
- c2 = 24 100
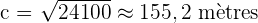
A c-ből eztán gyököt vonunk, így megkapjuk, hogy a labda és a lyuk közötti közvetlen távolság körülbelül 155,2 méter.
🏌️♂️ Amellett, hogy a Pitagorasz-tétel segít meghatározni a legjobb stratégiát a kívánt lyuk eléréséhez, lehetővé teszi a megfelelő ütő kiválasztását is, figyelembe véve a valódi távolságot.
A matektanárok nemcsak az iskolai feladatokban, hanem a mindennapi életben is segíthetnek alkalmazni a matematikai fogalmakat.
A sípálya lejtésének kiszámítása a lejtő meredeksége szerint
Azt hiszed, hogy a szögfüggvények nem jók semmire? Nagy tévedés! Az imént taglalt példa mellett a matematikai fogalmak ismerete egy sípálya lejtésének megértésében is a hasznodra válhat, különösen annak nehézségének felmérésében, hogy kiválaszthasd a megfelelő technikát.
A sánc lejtése egyszerű geometria segítségével, különösen a magasságkülönbség és a megtett vízszintes távolság mérésével számítható ki. A lejtés a sánc felülete és a vízszintes közötti szög. Ennek a szögnek a kiszámításához használhatjuk az tangensét, mert egy derékszögű háromszögben egy szög tangense az ellentétes oldal és a szomszédos oldal hányadosa.
Tegyük fel, hogy egy sípályán vagy, és ki akarod számolni a lejtést. Megméred, hogy egy 200 méteres vízszintes távolságon 50 métert fogsz ereszkedni. A lejtő szögének kiszámításához a tangens képletre lesz szükséged:
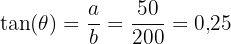
A szög meghatározásához egy szöggfüggvényt hívunk segítségül, amiből kiderül, hogy a sánc lejtési szöge körülbelül 14 fok.
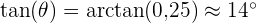
⛷️Ezekkel az információkkal jobban fel tudod mérni a lejtő nehézségét, és ennek függvényében megfelelően tudod beállítani a síelési technikádat. Ez azt is lehetővé teszi, hogy a tudásszintednek legjobban megfelelő lejtőket válaszd.
Az alapvető matematikai fogalmak felfrissítéséhez bármikor segítségedre vannak a Superprof matek magánórái!
Sportstatisztikák: labdarúgás és baseball
A matematika kulcsfontosságú a labdarúgásban a játékosok statisztikáinak, például a sikeres passzoknak és a kapura lövéseknek az elemzésében.
A csapatok a valószínűségszámítást használják arra, hogy megjósolják a játék kimenetelét, és ehhez igazítsák a stratégiájukat. A röppályaszámítások segítenek a pontos passzok és lövések előrejelzésében, optimalizálva az egyéni és a csapatteljesítményt a pályán.
Futballstatisztikák segítségével elemzett teljesítmény
A statisztikákat a játék különböző aspektusainak mérésére és értékelésére használják olyan értékes adatokat szolgáltatva a játékosok és az edzők számára, mint például a sikeres passzok száma, a sikeres gólok és a megtett kilométerek száma.

Tegyük fel, hogy egy középpályást több mérkőzésen keresztül követünk, és a következő adatokat kapjuk:
- Sikeres passzok: 85%
- Gólok száma: 40%
- Meccsenként megtett kilométerek: 10 km
- Ellenféltől elvett labdák meccsenként: 5
Ezen adatok elemzéséhez egyszerű statisztikai fogalmakat használhatsz. Tegyük fel, hogy egy játékos teljesítményét 5 mérkőzésen keresztül követed nyomon, és a sikeres passzokra vonatkozóan a következő adatokat gyűjtöd össze:
- 1. mérkőzés: 80%-os sikerráta
- 2. mérkőzés: 90%-os sikerráta
- 3. mérkőzés: 85%-os sikerráta
- 4. mérkőzés: 88%-os sikerráta
- 5. mérkőzés: 82%-os sikerráta
A sikeres passzok átlagos számának kiszámításához add össze a százalékokat, és oszd el a mérkőzések számával:
- 80+90+85+88+82 = 425
- 425/5 = 85%
Más szempontokat is elemezhetsz, például a teljesítmény változékonyságát. A következetesség értékeléséhez kiszámíthatod a sikeres passzok szórását. Az alacsony változékonyság következetesebb teljesítményt jelez.
⚽️ Ez a matematikai megközelítés lehetővé teszi a teljesítmény konkrét és mérhető javítását, így a statisztikai elemzés alapvető fontosságú a labdarúgók képességeinek fejlesztéséhez. Kérd meg hát matektanárodat vagy edződet, hogy ezzel is foglalkozzatok a matekórán vagy az edzésen!
A siker valószínűsége a baseballban
A statisztikák értékes információkkal szolgálnak a játékosok és csapatok teljesítményéről, míg a valószínűségek segítenek megjósolni a játékmenetek alakulását.
Tegyük fel, hogy egy játékos ütőteljesítményét szeretnénk elemezni. Számos szempont alapján gyűjthetsz adatokat, például a biztos ütések száma, a bázisra jutások száma (OBP = on-base percentage, vagyis a bázisra jutási százalék), a hazafutások száma és így tovább. Íme egy példa egy játékos adataira egy szezonra vonatkozóan:
- Sikeres találatok: 150
- Ütések száma: 500
- Hazafutások: 30
- Bázisra jutások száma: 200
Egy játékos ütésátlagának kiszámításához a sikeres találatok számát el kell osztani az ütések számával, vagyis ütésátlag = 150/500= 0,300.
Az on-base százalék (OBP) kiszámításához a játékos bázisra jutásainak számát kell elosztani az összes ütésszámmal, vagyis on-base százalék = 200/500 = 0,400.
A valószínűségszámítást használhatod bizonyos cselekvések előrejelzésére is. Ha például tudjuk, hogy egy játékosnak 500 ütés alatt 30 hazafutása van, akkor annak valószínűsége, hogy a következő ütésénél hazafutást várható, a következő: hazafutás = 30/500 = 0,06, azaz 6%.
A valószínűségek a mérkőzés közbeni valós idejű döntéshozatalban is segíthetnek. Ha például az adatok azt mutatják, hogy egy játékos nagyobb valószínűséggel fog eltalálni egy bizonyos típusú dobást, a dobó ennek megfelelően módosíthatja a stratégiáját.
Aritmetikai számítások: sebesség a teniszben
A matematika elengedhetetlen a teniszben a labda sebességének, az ütés szögének és a megtett távolságnak a kiszámításához.

A játékosok trigonometrikus számításokat használnak a pozícióik és a lövési szögek beállításához. A teljesítmény statisztikai elemzése segít felmérni az erősségeket és gyengeségeket, így könnyebbé válik a stratégia és az ütés pontosságának javítása a pályán.
A labda sebessége teniszben
Tegyük fel, hogy ki akarod számítani a tenisz szervád sebességét. Feljegyezted, hogy a labda 20 métert tett meg az ütődtől a pálya másik oldaláig, és 1 másodpercre időzítetted az adogatást. A labda sebességének kiszámításához a következő képletet használhatod: sebesség = távolság/idő.
Ezt a képletet alkalmazva a 20 méteres távolság és 1 másodperces idő alkalmazásával ezt kapod: sebesség = 20 méter/1 másodperc = 20 m/s.
A szerva javítása érdekében több edzésen keresztül is nyomon követheted a szervád sebességét. Ezt így teheted meg:
- Mérd a labda idejét több szervaütés során.
- Jegyezd fel a labda által megtett távolságot minden egyes ütésnél.
- Használd ezeket az adatokat az egyes ütések sebességének kiszámításához, és kövesd nyomon a fejlődését az idő múlásával.
Tegyük fel, hogy három különböző fonákütésnél megmérted a labda által megtett távolságot:
- 1. fonákütés: 15 m 0,75 s alatt
- 2. fonákütés: 14 m 0,70 s alatt
- 3. fonákütés: 16 m 0,80 s alatt
Az egyes szervák sebességének megállapítása tehát így néz ki:
- 1. fonákütés: 15 m/0,75 s = 20 m/s
- 2. fonákütés: 14 m/0,7 s =20 m/s
- 3. fonákütés: 16 m/0,8 s = 20 m/s
🎾 Ezekkel a számításokkal felmérheted az adogatási sebességed állandóságát és meghatározhatod a javítandó területeket. Ez lehetővé teszi, hogy célzottan dolgozz egy hatékonyabb és erőteljesebb adogatási technika kifejlesztésén, ami elengedhetetlen a teniszpályán való sikerhez.
Cikkünket elolvasva soha többé nem fogsz ugyanúgy tekinteni a matekórákra, mint azelőtt! A különféle adatok elemzése és a teljesítmény optimalizálása matematikai számításokkal nagyban hozzájárulnak a játékosok erősségeinek és gyengeségeinek feltárásához, amellyel javíthatók a stratégiai döntések, például a lövések, passzok vagy a mozgások pontos végrehajtása. A matek tehát a sport szerves részét képezi!
Ha te is szeretnél jobban elmélyedni a matematikában, és kihasználni annak erejét, például az adatelemzés vagy statisztikai számítások terén, egy online matematika tanfolyam segíthet abban, hogy kényelmesen és hatékonyan fejleszd a tudásodat. A Superprof platformon számos tapasztalt matematikai oktató közül választhatsz, akik segítenek a matek alapjaitól egészen a bonyolultabb témákig, online órák keretében. Akár a sportteljesítmény optimalizálásához, akár más területeken szeretnéd használni a matematikát, itt megtalálhatod a megfelelő segítséget!
Összefoglalás AI segítségével















